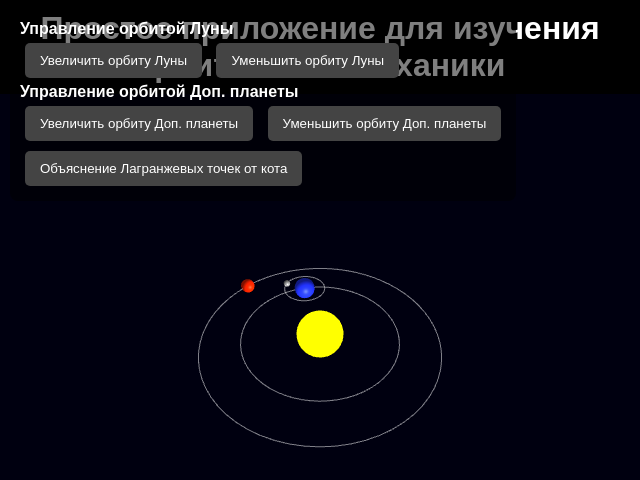
App 3D per la meccanica orbitale
dettagli
riepilogo
Applicazione 3D educativa per bambini sulla meccanica orbitale.
tag
prompt
Crea una semplice applicazione 3D per studiare la meccanica orbitale con controlli intuitivi, adatta a un bambino di 8 anni. Panoramica del progetto - Progetta un'app educativa incentrata sull'insegnamento dei fondamenti della meccanica orbitale, con la possibilità di controllare e visualizzare orbite in 3D. UI/UX Design e flusso - Sviluppa un'interfaccia intuitiva con elementi visivi chiari e controlli semplici per i bambini. - Includi pulsanti per aumentare o diminuire il raggio delle orbite di vari corpi celesti. - Assicurati che tutti gli oggetti siano in costante movimento lungo le loro orbite per migliorare l'apprendimento. Funzionalità chiave e logica - Modella la Terra, la Luna e altri pianeti con traiettorie orbitali distinte. - Visualizza le traiettorie utilizzando linee sottili che rappresentano le orbite. - Integra una funzione che aggiorna dinamicamente la visualizzazione al variare del raggio orbitale. Best practices - Concentrati nel fornire un'esperienza educativa e coinvolgente. - Assicura una rappresentazione accurata dei principi della meccanica orbitale. - Mantieni l'interfaccia intuitiva e facile da usare per i più piccoli. - Utilizza un linguaggio semplice e grafiche chiare per spiegare concetti complessi. Includi risorse che spieghino la meccanica orbitale in modo accessibile per i bambini, utilizzando analogie comprensibili e visualizzazioni chiare, e offri elementi interattivi come la spiegazione dei punti di Lagrange dalla prospettiva di un gatto per catturare l'attenzione del pubblico target.
prompt originale
Создай простое приложение для изучения орбитально механики с возможностьюь контроля орбит итд. все должно быть в 3д и наглядно чтобы даже 8 летний ребенок понял. LAGRANGE POINTS EXPLAINED BY A CAT Lagrange Points are spots where gravity and motion balance out. L1, L2, L3 sit on the line. L1: between Earth and Moon. L3: beyond Moon. L3: opposite Earth. L2 - L5 L3 L4 and L5 form equilateral triangles with Earth and Moon. Stable zones-gravity traps for space chill. # Обязательно все обьекты должны двигаться по своим орбитам. # Нужно визуализировать траектории тонкой линией # Нужны контролы, чтобы можно было изменять радиусы орбит всех планет и динамически менять визуализацию Q: Какой интерфейс управления вы представляете для изменения радиусов орбит? A: Кнопки для увеличения/уменьшения радиуса. Q: Какие планеты или объекты вы хотите включить в приложение? A: Земля, Луна и другие планеты.
riepilogo dei costi di generazione
nome del modello: o3-mini-high
tempo di risposta: 114.53 sec.
token di risultato: 16,433
costo: $0.07299490